La circunferencia

¿Qué es una circunferencia?

De manera formal, una circunferencia se define como el lugar geométrico de los puntos del plano equidistantes de otro, llamado centro de la circunferencia.

No debemos nunca confundir el concepto de círculo con el concepto de circunferencia, que en realidad una circunferencia es la curva que encierra a un círculo (la circunferencia es una curva, el círculo una superficie).

A continuación vemos una imagen de una circunferencia.

En realidad, y de manera más sencilla, una circunferencia es el conjunto de puntos situados en el plano todos a la misma distancia de un mismo punto central, al que llamaremos centro, y del que hablaremos más adelante con detalle en la parte de elementos básicos de la circunferencia.

Elementos básicos

En la imagen expuesta arriba se pueden ver todos los elementos que vamos a nombrar a continuación:

• Centro: punto central que está a la misma distancia de todos los puntos pertenecientes a la circunferencia.
• Radio: pedazo de recta que une el centro con cualquier punto perteneciente a la circunferencia.
• Cuerda: pedazo de recta que une dos puntos cualquiera de una circunferencia.
• Diámetro: mayor cuerda que une dos puntos de una circunferencia. Hay infinitos diámetros y todos pasan por el centro de la circunferencia.
• Recta secante: recta que corta dos puntos cualesquiera de una circunferencia.
• Recta tangente: recta que toca a la circunferencia en un solo punto y es perpendicular a un radio.   

Problemas

Indica, atendiendo a la descripción proporcionada, de que elemento de la circunferencia se trata:

C: segmento que une dos puntos cualesquiera de la circunferencia.

r: segmento que une el centro con cualquier punto perteneciente a la circunferencia.

o: punto del plano que está a la misma distancia de todos los puntos pertenecientes a la circunferencia.

D: la cuerda mas grande que existe en una circunferencia.

S: recta que corta dos puntos cualesquiera de la circunferencia.

Desarrollo:

Los elementos de la figura son los siguientes:

C es una cuerda, elemento que une dos puntos cualquiera de la circunferencia.

r es el radio de la circunferencia.

s es el centro de la circunferencia.

D es el diámetro de la circunferencia, la cuerda más larga.

S es una recta secante a la circunferencia.

Solución:

C: cuerda, r: radio, o: centro, D: diámetro, S: recta secante.

Posiciones relativas de dos circunferencias:

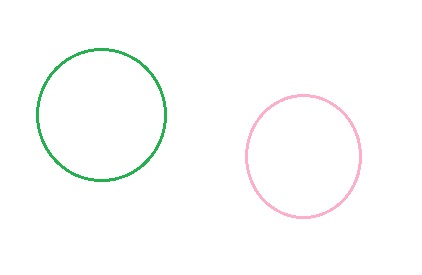
• Circunferencias exterioresSon las que no tienen ningún punto en común y cada una esta en una región exterior a la otra.

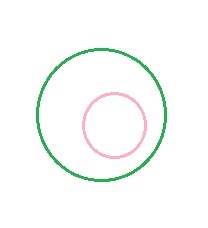
• Circunferencias interiores
  No tienen ningún punto en común y una está en la región interior de la otra.

• Circunferencias tangentes exterioresTienen un punto en común y los demás puntos de cada una de ellas están en la región exterior de la otra.

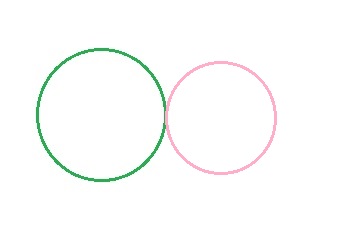
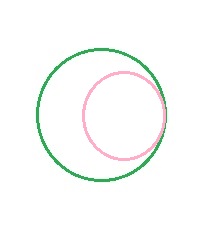
• Circunferencias tangentes interioresTienen un punto en común y los demás puntos de una de ellas están en la región interior de la otra.

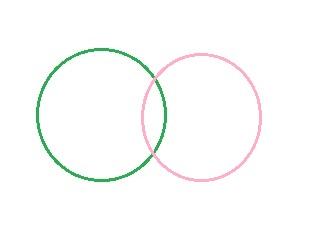
• Circunferencias secantesTienen dos puntos en común.

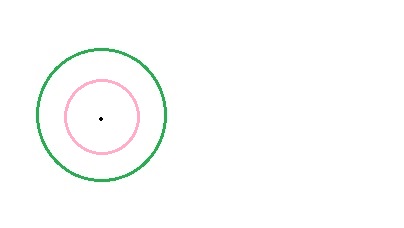
• Circunferencias concéntricasNo tienen ningún punto en común, una esta en el interior de la otra y tienen el mismo centro pero distinto radio.

Posiciones relativas de una recta y una circunferencia: una recta puede estar respecto a una circunferencia:

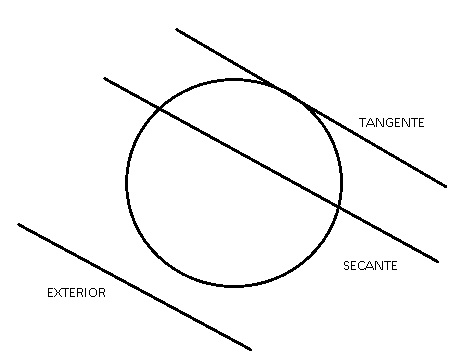
• Recta exterior: cuando no tiene ningún punto común con la circunferencia.
• Recta tangente: a la circunferencia cuando tiene un punto común.
• Recta secante: a la circunferencia cuando tiene dos puntos comunes.

Ángulos de la circunferencia:

• Ángulo centralEs el ángulo que tiene su vértice en el centro y sus lados lo forman dos radios.

-Si dos ángulos centrales son iguales también lo son los arcos correspondientes.
-La medida de un arco central es la misma que la de su ángulo central correspondiente.

• Ángulo inscritoEs aquel que tiene su vértice en la circunferencia y sus lados son secantes a ella.

-La medida de un ángulo inscrito es igual a la mitad del arco que abarca.

• Ángulo semi-inscrito
  Es aquel que tiene su vértice en un punto de la circunferencia y un lado es tangente y el otro secante a ella.

- La medida de un ángulo semi-inscrito es la mitad del arco que abarca. 

• Ángulo interiorEs aquel que tiene su vértice en un punto interior del círculo. Sus lados con cuerdas de la circunferencia.

-Un ángulo interior mide la mitad de la suma de las medias de su arcos que abarcan su lados y las prolongaciones de los mismos. 

• Ángulo exteriorEs aquel que tiene su vértice en un punto fuera de la circunferencia y del circulo y su lados son secantes o tangentes de la circunferencia.

- La medida de un ángulo exterior es la mitad de la diferencia de los arcos que abarca el ángulo.

.

ECUACIÓN GENERAL DE LA CIRCUNFERENCIA.

Si conocemos el centro y el radio de una circunferencia, podemos construir su ecuación ordinaria, y si operamos los cuadrados, obtenemos la forma general de la ecuación de la circunferencia, así: Demostración: Ejemplo: Hallar la ecuación general de la circunferencia con centro C(2;6) y radio r = 4 (x - 2)² + (y - 6)² = 4² X² - 2(2x) + 2² + y² - 2(6y) + 6² = 4² X² - 4x + 4 + y² - 12y + 36 = 16 X² + y² - 4x - 12y + 4 + 36 - 16 =0 X² + y² - 4x - 12y + 24 = 0